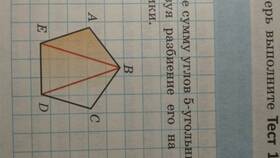
Сумма внутренних углов любого выпуклого многоугольника определяется строгими геометрическими законами. Рассмотрим подробно, как вычисляется этот показатель для семнадцатиугольника.
Содержание
Общая формула для выпуклых многоугольников
Для любого выпуклого n-угольника сумма внутренних углов (S) вычисляется по формуле:
| S = (n - 2) × 180° | где n - количество сторон (углов) многоугольника |
Расчет для семнадцатиугольника
Применим формулу для n = 17:
- Подставляем значение в формулу: S = (17 - 2) × 180°
- Вычисляем разность в скобках: 17 - 2 = 15
- Умножаем на 180°: 15 × 180° = 2700°
Проверка правильности расчета
| Количество сторон | Сумма углов | Проверка |
| Треугольник (3) | 180° | (3-2)×180°=180° |
| Четырехугольник (4) | 360° | (4-2)×180°=360° |
| Пятиугольник (5) | 540° | (5-2)×180°=540° |
| 17-угольник (17) | 2700° | (17-2)×180°=2700° |
Вычисление величины одного угла правильного семнадцатиугольника
Для правильного семнадцатиугольника (со всеми равными сторонами и углами):
- Сумма всех углов: 2700°
- Количество углов: 17
- Величина одного угла: 2700° ÷ 17 ≈ 158,82°
Историческая справка
Интересные факты о семнадцатиугольниках:
- Правильный семнадцатиугольник можно построить с помощью циркуля и линейки
- Это доказал Карл Фридрих Гаусс в 1796 году
- 17-угольник относится к простым числам Ферма в геометрии
- Имеет теоретическое значение в теории чисел и алгебраической геометрии
Практическое применение
Хотя 17-угольники редко встречаются в повседневной жизни, они важны:
- В архитектурных экспериментах
- При создании специальных оптических систем
- В криптографии и кодировании информации
- Как математический объект для исследований
Заключение
Сумма внутренних углов выпуклого семнадцатиугольника составляет 2700 градусов. Этот результат получен по общей формуле для выпуклых многоугольников и подтверждается логикой геометрических построений. Знание таких закономерностей расширяет понимание геометрических свойств сложных фигур.