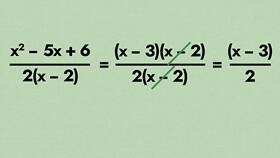- Вынесение общего множителя за скобки
- Группировка подобных слагаемых
- Использование формул сокращенного умножения
- Применение свойств арифметических операций
- Разложение на простые компоненты
| Исходное выражение | 3x + 5y + 2x - 3y |
| После упрощения | 5x + 2y |
| Исходное выражение | 2(a + b) + 3(a - b) |
| После упрощения | 5a - b |
- Идентифицируйте все слагаемые в выражении
- Найдите общие множители или подобные члены
- Примените распределительный закон умножения
- Сгруппируйте одинаковые переменные
- Выполните арифметические операции
- Проверьте результат на возможность дальнейшего упрощения
| Квадрат суммы | (a + b)² = a² + 2ab + b² |
| Квадрат разности | (a - b)² = a² - 2ab + b² |
| Сумма кубов | a³ + b³ = (a + b)(a² - ab + b²) |
| Разность кубов | a³ - b³ = (a - b)(a² + ab + b²) |
Пример упрощения числовой суммы
| Исходное выражение | 12 + 18 + 6 + 24 |
| Шаг 1: Нахождение НОД | НОД(12,18,6,24) = 6 |
| Шаг 2: Вынесение общего множителя | 6 × (2 + 3 + 1 + 4) |
| Результат | 6 × 10 = 60 |
- Финансовые расчеты и бюджетирование
- Статистический анализ данных
- Инженерные вычисления
- Программирование и алгоритмы
- Научные исследования
Освоение техник упрощения сумм значительно повышает эффективность математических вычислений и помогает находить оптимальные решения сложных задач. Регулярная практика с различными типами выражений развивает навык быстрого анализа и преобразования математических конструкций.
